ปัญหาระคน

จำนวนนับ คือ จำนวนที่นับสิ่งของต่างๆ ซึ่งแบ่งออกเป็น 2 ประเภทคือ จำนวนคู่ คือ จำนวนที่หารด้วย 2 ลงตัว และ จำนวนคี่ คือ จำนวนที่หารด้วย 2 ไม่ลงตัว เช่น 1, 3, 5,.....

ตัวประกอบเฉพาะ คือ ตัวประกอบของจำนวนนับที่เป็นจำนวนเฉพาะ
ตัวประกอบ คือ จำนวนนับใดๆที่หารจำนวนนับนั้นลงตัวเช่น ตัวประกอบของ 10 คือ 1 , 2 , 5และ10
ตัวหารร่วมมาก คือ จำนวนนับใดๆที่เป็นตัวประกอบร่วมที่มีค่ามากที่สุดของจำนวนนับนั้น
เขียนย่อคือ ห.ร.ม. เช่น ตัวประกอบร่ามมากสุดของ 16 และ 24 คือ 8
จำนวนเฉพาะ คือ จำนวนนับที่มากกว่า 1 และมีตัวประกอบเพียงสองตัวเท่านั้นได้แก่ 1 และตัวมันเอง เช่น จำนวนเฉพาะที่อยู่ระหว่าง 1 ถึง 10 คือ 2 , 3 , 5 , 7
การแยกตัวประกอบ คือ ประโยคที่แสดงการเขียนจำนวนนับนั้นในรูปการคูณของตัวประกอบ เฉพาะ เช่น ตัวประกอบของ 12 คือ 2 * 2 * 3
ตัวคูณร่วมน้อย คือ จำนวนนับใดๆที่เป็นตัวประกอบร่วมที่มีค่าน้อยที่สุดของจำนวนนับ
เขียนย่อคือ ค.ร.น. เช่น ตัวคูณร่วมน้อยของ 4 และ 6 คือ 12 ตัวประกอบของจำนวนนับ จำนวนที่นักเรียนพบเห็นในชีวิตประจำวันอยู่เสมอๆได้แก่ 1,2,3,4,……ไม่มีที่สิ้นสุด เรียกจำนวนเหล่านี้ว่า จำนวนนับ หรือ จำนวนธรรมชาติ หรือ จำนวนเต็มบวก จงพิจารณาตารางต่อไปนี้

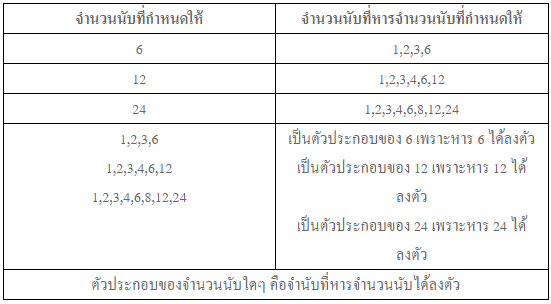
การแยกตัวประกอบ จงพิจารณาตารางต่อไปนี้

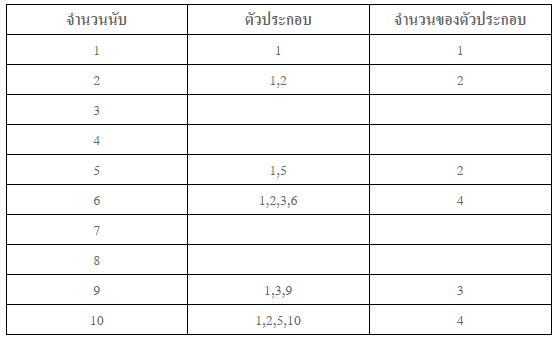
จากตารางข้างต้น  จะเห็นว่าจำนวนนับที่กำหนดให้แต่ละจำนวน  สามารถเขียนในรูปการคูณได้หลวกหลาย
พิจารณาแบบที่ 2 จะเห็นว่า
                        8 = 2 x 2 x 2  ตัวคูณ คือ 2  แต่ละจำนวนเป็นตัวประกอบ
                        12 = 2 x 2 x 3  ตัวคูณ คือ 2 และ 3  แต่ละจำนวนเป็นตัวประกอบ
เช่นเดียวกัน  20 = 2 x 2 x 5 ตัวคูณ คือ 2 และ 5  แต่ละจำนวนเป็นตัวประกอบ
เราเรียกประโยค  8 = 2 x 2 x 2 ว่าเป็นการแยกตัวประกอบของ 8
                       12 = 2 x 2 x 3 ว่าเป็นการแยกตัวประกอบของ 12
                       20 = 2 x 2 x 5 ว่าเป็นการแยกตัวประกอบของ 20
                การแยกตัวประกอบของจำนวนนับใด คือ ประโยคที่แสดงการเขียนจำนวนนับในรูปการคูณของตัวประกอบเฉพาะ ประโยค  28 = 2 x 2 x 7  แสดงการเขียน 28 ในการคูณของตัวประกอบเฉพาะเราเรียกประโยคนี่ว่า  การแยกตัวประกอบของ 28
ตัวอย่าง  จงแยกตัวประกอบของ 225
วิธีทำ                      225 = 3 x 3 x 5 x 5 

ตัวหารร่วมมาก  หรือ ห.ร.ม (Greatest  common  divisor: G.C.D)
                การหารร่วมมาก ที่จะกล่าวต่อไปนี้จะนำเสนอวิธีการหารเพียง 3 วิธีเท่านั้น  คือ การหาร ห.ร.ม โดยวิธีการพิจารณาตัวประกอบ การหา ห.ร.ม โดยการแยกตัวประกอบ  และการหา ห.ร.ม โดยการตั้งหาร 
(หารสั้น) เราจะยกตัวอย่างการหา ห.ร.ม โดยวิธีการพิจารณาตัวประกอบเท่านั้น
การหา ห.ร.ม โดยวิธีการพิจารณาตัวประกอบ
           พิจารณาตัวประกอบของ 12 และ 18 มาเขียนแสดงความสัมพันธ์ใหม่ ดังนี้
ตัวประกอบของ 12 คือ 1,2,3, และ 4,6,12
ตัวประกอบของ 18 คือ 1,2,3, และ 6,9,18
ตัวประกอบร่วม( Common factor ) ของ 12 และ 18 ได้แก่ 1,2,3,6

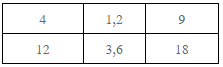
ตัวประกอบร่วมของ 12 และ 18 ที่มากที่สุดได้แก่ 6
เรียกตัวประกอบร่วมที่มากที่สุดว่า  ตัวหารร่วมมาก 
ดังนั้น 6 เป็นตัวหารร่วมมากของ 12 และ 18 หรือ 6 เป็น ห.ร.ม ของ 12 และ 18
ตัวประกอบร่วมที่มีค่ามากที่สุดของจำนวนนับนั้น เรียกว่า ตัวหารร่วมมาก (ห.ร.ม)
สรุป   การหา ห.ร.ม โดยวิธีการพิจารณาตัวประกอบ ทำได้โดยหาตัวประกอบร่วมของทุกจำนวนและ
พิจารณาตัวประกอบร่วมที่มากที่สุด ห.ร.ม ของจำนวนนับคือ  ตัวประกอบร่วมที่มากที่สุด
ตัวอย่าง  จงหา  ห.ร.ม ของ 18 และ 48
วิธีทำ    ตัวประกอบของ 18 ได้แก่ 1,2,3,6,9 และ 18
                ตัวประกอบของ 48 ได้แก่ 1,2,3,4,6,8,12,16,24 และ 48
                ตัวประกอบร่วมของ 18 และ 48 ได้แก่ 1,2,3,6
                ตัวประกอบร่วมของ 18 และ 48 ที่มากที่สุดได้แก่ 6
ดังนั้น ห.ร.ม ของ 18 และ 48 คือ 6 

การคูณร่วมน้อย หรือ ค.ร.น (Least  common  multiple: L.C.M)
                การหาตัวคูณร่วมน้อย ที่กล่าวต่อไปนี้จะนำเสนอวิธีการหาเพียง 3 วิธีเท่านั้น  คือการหา ค.ร.น โดยวิธีการพิจารณาพหุคูณ  การหา ค.ร.น โดยการแยกตัวประกอบและการหา 8 ค.ร.น โดยการแยกตัวประกอบและการหา ค.ร.น  โดยการตั้งหาร( หารสั้น ) ในที่นี่จะยกตัวอย่างกรณีเดี๋ยว คือ
การหา ค.ร.น โดยวิธีการพิจารณาพหุคูณ
     ให้นักเรียนช่วยกันพิจารณา  ดังนี้
                พหุคูณของ 3 คือ 3,6,9,12,15,18,21,24,30,33,36,…
                พหุคูณของ 5 คือ 5,10,15,20,25,30,35,40,45,50,….
                พหุคูณร่วมของ 3 และ 5 ได้แก่ 15,30,45,….
                พหุคูณร่วมน้อยที่สุดของ 3 และ 5 ได้แก่ 15
                เรียกพหุคูณที่น้อยที่สุดว่า ตัวคูณร่วมน้อย
                ดังนั้น 15 เป็นตัวคูณร่วมน้อยของ 3 และ 15
                เขียนย่อๆว่า 15 เป็น ค.ร.น ของ 3 และ 5
สรุป     การหา ค.ร.น โดยวิธีพิจารณาพหุคูณทำได้โดยหาจำนวนที่มีจำนวนที่กำหนดให้เป็นตัวประกอบ  แล้วพิจารณาจำนวนที่น้อยที่สุดที่มีจำนวนเหล่านั้นเป็นตัวประกอบ ค.ร.น ของจำนวนนั้น  คือ จำนวนที่น้อยที่สุดที่มีจำนวนเหล่านั้นเป็นตัวประกอบ

http://theeranan13.blogspot.com/2013/08/2-2-2-1-10-1-2-5-10.html