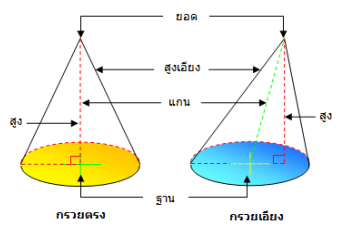
กรวย (Cone) หมายถึง รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรง

ปริมาตรของกรวย = 1/3(πr2h) (เมื่อ r คือรัศมีของฐานกรวย และ h คือส่วนสูงของกรวย)

พื้นที่ผิวกรวย = πr(r + h) (เมื่อ r คือรัศมีของฐานกรวย และ h คือส่วนสูงของกรวย)

หลักในการทำโจทย์พื้นที่ผิว-ปริมาตรของกรวย

1. แทนค่าตามสูตรให้ถูกต้อง และในการคำนวณแทนค่า π ตามโจทย์ หรือถ้าโจทย์ไม่กำหนด สามารถติดในรูป π ไว้ได้
2. การคำนวณเกี่ยวกับเรื่องกรวยตัดยอดสามารถใช้อัตราส่วนปริมาตรและอัตราส่วนด้านที่สมนัยหรือใช้สามเหลี่ยมคล้ายมาช่วย
3. การหาปริมาตรของเหลวที่บรรจุอยู่ภายในกรวย ใช้หลักการเดียวกับการคำนวณปริมาตรกรวยตัดยอด
4. การประยุกต์กรวยในรูปแบบต่างๆ ให้ยึดส่วนสูงกรวยและรัศมีฐานของกรวยด้วย
5. สามารถประยุกต์กรวยกับทรงกระบอกได้ เพราะ ทรงกระบอกมีปริมาตรเป็น 3 เท่าของปริมาตรกรวย

ตัวอย่าง      เซกเตอร์วงกลมอันหนึ่งทำมุมที่จุดศูนย์กลาง 135 องศา มีรัศมี 64 เซนติเมตร นำมาทำเป็นกรวย จงหาปริมาตรกรวยที่                        ได้จากเซกเตอร์นี้

วิธีทำ          

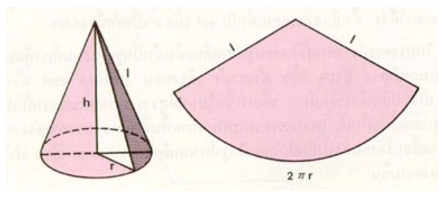
จากรูป      l = 64,  เนื่องจากมุมที่จุดศูนย์กลางมีขนาด 135 องศา จะมีพื้นที่คิดเป็น 135/360 = 3/8 เท่าของวงกลม

ดังนั้น เส้นรอบวงก็จะต้องยาว 3/8 เท่าของวงกลมเช่นกัน จากเส้นรอบวงกลม    =     2πR เมื่อ R คือรัศมีของวงกลม

               จะได้ว่า เซกเตอร์มีส่วนโค้งยาว      3/8 × 2π(64)      =       48π เซนติเมตร

จากรูป      r     =     48π/2π      =      24 เซนติเมตร โดยทฤษฎีบทพีทากอรัส ;      h2      +       r2       =      l2

จะได้     h2     =        4096 – 576       =      3520 ;      h       =       8(551/2) เซนติเมตร

ปริมาตรกรวย      =     1/3(πr2h)      (เมื่อ r คือรัศมีของฐานกรวย และ h คือส่วนสูงของกรวย)

           =      1/3(π)(576)(8(551/2))       =       1536(551/2)π ลูกบาศก์เซนติเมตร

ตอบ       กรวยมีปริมาตร  1536(551/2)π ลูกบาศก์เซนติเมตร

ตัวอย่าง       กรวยตัดยอดอันหนึ่งมีรัศมีส่วนบน 7 หน่วย และมีรัศมีฐาน 14 หน่วย มีส่วนสูง 22 หน่วย จงหาปริมาตรของกรวยตัด                                ยอดอันนี้

วิธีทำ        พิจารณาโจทย์ สามารถคิดปริมาตรกรวยตัดยอดจากหลักการสามเหลี่ยมคล้ายกับอัตราส่วนด้านที่สมนัย

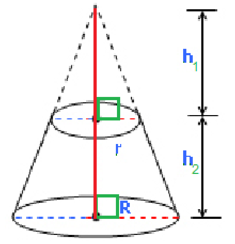
  จากรูปจะได้ว่า       r/R        =          h1/(h1 + h2);         7/14       =       h1/(h1 + 22)

7(h1 + 22)          =       14(h1)

                        154          =       7(h1)

ดังนั้น      h1      =       22 หน่วย      เห็นชัดว่ากรวยถูกตัดครึ่ง ดังนั้น กรวยตัดยอดมีปริมาตร

1/3(π)(72)(22)        =              1/3(π)(49)(22)         =        1078/3(π) ลูกบาศก์หน่วย

ตอบ      กรวยตัดยอดมีปริมาตร  1078/3(π) ลูกบาศก์หน่วย

https://mathsm3areaandvolume.wordpress.com/2015/08/30/กรวย-cone/